Algebra di Boole

Da Wikipedia, l'enciclopedia libera.

Vai a: Navigazione, cerca

   

In matematica, informatica ed elettronica, l'algebra di Boole, anche detta algebra booleana o reticolo booleano, è un ramo dell'algebra astratta che comprende tutte le algebre che operano con i soli valori di verità 0 o 1, detti variabili booleane o logiche. La struttura algebrica studiata dall'algebra booleana è finalizzata all'elaborazione di espressioni nel'ambito del calcolo proposizionale.
Essendo un reticolo dotato di particolari proprietà, l'algebra booleana risulta criptomorfa, cioè associata biunivocamente e in modo da risultare logicamente equivalente, ad un insieme parzialmente ordinato reticolato. Ogni algebra booleana risulta criptomorfa ad un particolare tipo di anello, chiamato anello booleano.
Tale algebra permette di definire gli operatori logici AND, OR e NOT, la cui combinazione permette di sviluppare qualsiasi funzione logica e consente di trattare in termini esclusivamente algebrici le operazioni insiemistiche dell'intersezione, dell'unione e della complementazione, oltre a questioni riguardanti singoli bit 0 e 1, sequenze binarie, matrici binarie e diverse altre funzioni binarie.
L'algebra di Boole, sviluppata nel 1854 da George Boole, un matematico inglese dell'University College di Cork, assume un ruolo importante in vari ambiti, in particolare nella logica matematica e nell'elettronica digitale, dove nella progettazione dei circuiti elettronici riveste grande importanza il teorema di Shannon, introdotto da Claude Shannon intorno al 1940 e utilizzato per suddivire una funzione booleana complessa in funzioni più semplici, o per ottenere un'espressione canonica da una tabella della verità o da un'espressione non canonica.

Indice [nascondi] 1 Definizione 2 Basi 2.1 Reticolo 2.2 Anello 2.3 Sheffer stroke 3 Operatori booleani 3.1 NOT 3.2 OR 3.3 AND 3.4 XOR 3.5 NOR 3.6 NAND 3.7 XNOR 4 Esempi 5 Omomorfismi ed isomorfismi 6 Espressioni booleane 7 Rappresentazione delle algebre booleane 8 Voci correlate 9 Collegamenti esterni

Definizione

L'algebra di Boole tratta l'algebra universale dell'algebra a due stati e dei modelli di tale teoria, detti algebre booleane. L'algebra universale è la famiglia di operazioni su un insieme, detto insieme fondamentale della famiglia algebrica, che nel caso della struttura algebrica booleana contiene i soli valori 0 e 1.
Il numero degli argomenti che richiede una funzione sull'insieme fondamentale è detto arietà: un'operazione su {0,1} di arietà n può essere applicata ad ognuno dei 2ⁿ possibili valori dei suoi n argomenti. Per ogni scelta di argomenti l'operazione può produrre i soli risultati 0 e 1, donde ci sono 2²ⁿ operazioni di n argomenti.
L'algebra a due stati possiede due operazioni con nessun argomento, i valori 0 e 1, e quattro operazioni con un solo argomento: due operazioni costanti, l'identità e la negazione, ques'tultima da come risultato 0 se l'argomento è 1 e viceversa. Vi sono poi sedici operazioni binarie: due costanti, due che danno come risultato rispettivamente solo il primo argomento e solo il secondo, la congiunzione, che produce 1 se entrambi gli argomenti sono 1 e dà 0 altrimenti; la disgiunzione, che produce 0 se entrambi gli argomenti sono 0 e dà 1 altrimenti; e così via. Il numero di operazioni con n+1 argomenti è il quadrato del numero delle operazioni con n argomenti, sicché vi sono 16² = 256 operazioni ternarie, 256² = 65,536 operazioni quaterniarie e così via.
Una famiglia, detta anche indice, è indicizzata da un insieme di indici, che nel caso di una famiglia di operazioni costituenti un'algebra sono detti simboli dell'operazione e costituiscono il linguaggio dell'algebra in oggetto. L'operazione indicizzata da un dato simbolo è detta interpretazione di tale simbolo, ed ogni simbolo definisce il numero univoco di argomenti delle rispettive interpretazioni possibili. Nel caso considerato vi è una corrispondenza biunivoca tra simbolo e interpretazione. L'algebra di Boole ha 2²ⁿ simboli, e dunque lo stesso numero di
operazioni, detti simboli di operazione booleana; anche se poche operazioni hanno simboli convenzionali, quali ¬ per la negazione, ∧ per la congiunzione e ∨ per la disugiunzione. In generale si indica con ⁿf_i l'i-esimo simbolo di n argomenti.

Basi

Una base è un insieme di operazioni la cui composizione permette di ottenere tutte le operazioni appartenenti all'algebra. Le tre principali basi usate nell'algebra booleana sono:

• Il reticolo, una base logica introdotta nel diciannovesimo secolo da George Boole, Charles Sanders Peirce e altri matematici che cercavano una formalizzazione algebrica dei processi logici.
• L'anello booleano, una base aritmetica introdotta nel ventesimo secolo da Ivan Ivanovich Zhegalkin e Marshall Stone che proviene dall'algebra astratta.
• La base Sheffer stroke, anche detta NAND, originata dal fatto che tramite l'operazione di NAND è possibile ottenere tutte le operazioni sull'insieme {0,1}. Tale base è utilizzata in particolare nella configurazione dei circuiti logici in elettronica digitale.

Gli elementi comuni a reticolo e anello sono le costanti 0 e 1 ed un'operazione binaria associativa e commutativa, che nella base del reticolo è detta incontro, dal termine inglese meet, e denotata tra due elementi x e y dal simbolo x∧y, mentre nella base dell'anello è detta moltiplicazione e denotata xy. La base del reticolo ha inoltre le operazioni algebriche di unione x∨y e complemento ¬x, mentre la base dell'anello ha l'ulteriore operazione aritmetica di addizione x⊕y o x+y.

Reticolo

Nella base del reticolo ad un'algebra booleana (A, , ) si associa un insieme parzialmente ordinato (A, ), definendo:

che è anche equivalente a

È possibile anche associare un'algebra booleana ad un reticolo distributivo (A, ), considerato come insieme parzialmente ordinato, dotato di elemento minimo 0 e di elemento massimo 1, in cui ogni elemento x ha un complementare 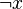tale che

e

Qui e sono usati per denotare l'inf ed il sup di due elementi. Se i complementi esistono, allora sono unici.

Anello

La base dell'anello della generica algebra booleana (A, , ) è definita come (A, +, *), definendo a + b := (a b) ( b a ). In tale anello l'elemento neutro per la somma coincide con lo 0 dell'algebra booleana, mentre l'elemento neutro della moltiplicazione è l'elemento 1 dell'algebra booleana. Questo anello ha la proprietà che a * a = a per ogni a in A; gli anelli con questa proprietà sono chiamati anelli booleani.
Viceversa, assegnato un anello booleano A, possiamo trasformarlo in un'algebra booleana definendo x y = x + y − x y e x y = x y. Poiché queste due operazioni sono l'una l'inversa dell'altra, possiamo affermare che ogni anello booleano è criptomorfo di un'algebra booleana e viceversa. Inoltre, una funzione f : A B è un omomorfismo tra algebre booleane se e soltanto se è un omomorfismo tra anelli booleani. La categoria degli anelli booleani e delle algebre booleane sono equivalenti.
Un anello ideale dell'algebra booleana A è un sottoinsieme I tale che per ogni x, y in I si ha x y in I e per ogni a in A a x in I. Questa nozione di ideale coincide con la nozione di anello ideale negli anelli booleani. Un ideale I di A è detto primo se I A e se a b in I implica sempre a in I o b in I. Un ideale I di A è detto massimale se I A e se l'unico ideale proprio contenente I è A stesso. Questa notazione coincide con la notazione teorica del ideale primo e ideale massimale nell'anello booleano A.
Il duale di un ideale è un filtro. Un filtro dell'algebra booleana A è un sottoinsieme F tale che per ogni x, y in F si ha x y in F e per ogni a in A se a x = a allora a è in F.
L'operazione di complementazione * applicata ai sottoinsiemi manda dunque gli ideali in filtri e viceversa: se B è un'algebra booleana e un suo ideale (proprio), allora è il filtro (proprio) duale di I. Se invece 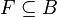è un filtro (proprio), l'ideale (proprio) duale di F.

Sheffer stroke

La base Sheffer stroke o NAND si basa sulle operazioni NOT e AND, tramite le quali è possibile ottenere tutte le operazioni booleane. Un'algebra booleana può essere definita sia da NOT e AND che da NOT e OR, essendo possibile definire OR attraverso NOT e AND così come AND attraverso NOT e OR:

La collezione di tutti i sottoinsiemi di un dato insieme, ovvero l'insieme delle parti o insieme ambiente, munita delle operazioni di unione, intersezione e complementazione di insiemi, che giocano rispettivamente il ruolo di OR, AND e NOT, costituisce un'algebra booleana.
Più formalmente, se B è un insieme formato da almeno 2 elementi, l'algebra booleana avente B come supporto è la struttura algebrica costituita da B, da due operazioni binarie su B, OR e AND, da un'operazione unaria NOT su B e dall'elemento 0 di B, i quali godono delle seguenti proprietà:

• Simmetria di AND:
• Simmetria di OR:
• Involuzione di NOT:
• Leggi di De Morgan:

L'insieme B è inoltre limitato inferiormente, essendo:

L'elemento 1 è definito come la negazione, o il complementare, dello 0: 1 := NOT(0). L'insieme B è dunque limitato superiormente, essendo:

ed in particolare

0 AND 1 = 0 ; 0 OR 1 = 1

Si definisce inoltre, come operazione derivata dalle precedenti, l'operatore binario OR esclusivo, denotato XOR:

In questa algebra all'operatore XOR corrisponde la differenza simmetrica:

In elettronica la porta logica NAND è costituita da n ingressi e un'uscita che si porta a livello 0 solo se gli n ingressi si portano a livello 1. È corrispondente alla connessione in serie di una porta AND e di una NOT.

Operatori booleani

Gli operatori dell'algebra booleana possono essere rappresentati in vari modi. Spesso sono scritti semplicemente come AND, OR e NOT. Nella descrizione dei circuiti, possono anche essere usati NAND (NOT AND), NOR (NOT OR) e XOR (OR esclusivo). In matematica spesso si usa + per OR e per AND, mentre si rappresenta il NOT con una barra segnata sopra l'espressione che viene negata.
Esistono diverse altre simbologie per rappresentare gli operatori, scelte in base al campo in cui si lavora: i matematici usano spesso il simbolo + per l'OR, e × per l'AND, in quanto per alcuni versi questi operatori lavorano in modo analogo alla somma e alla moltiplicazione. La negazione NOT viene rappresentata spesso da una linea disegnata sopra l'argomento della negazione, cioè dell'espressione che deve essere negata.
Nella progettazione di circuiti elettronici, vengono utilizzati anche gli operatori brevi NAND (AND negato), NOR (OR negato) e XNOR (XOR negato): questi operatori, come XOR, sono delle combinazioni dei tre operatori base e vengono usati solo per rendere la notazione più semplice.
Operatori:

• NOT - simboli alternativi: x, ~, ¬, !
• AND - simboli alternativi: AND: *, AND, ^, BUT (usato nella logica booleana insieme al NOT)
• OR - simboli alternativi: OR: +, OR, v
• XOR - simboli alternativi: XOR: +, ⊕, ∨, ^, EOR, orr
• NAND - simboli alternativi: NAND, ↑
• NOR - simboli alternativi: NOR, ↓
• XNOR

Valori:

• vero - simboli alternativi: true, 1, ON, SI (YES)
• falso - simboli alternativi: false, 0, OFF, NO

In elettronica digitale viene definito vero un bit 1, sia in Input che in Output, che di solito assume il valore di 5 V, mentre viene definito falso un bit 0, sia in Input che in Output, che assume il valore di 0 V.
Di seguito sono indicati gli operatori più comuni e le rispettive porte logiche:

NOT

L'operatore NOT restituisce il valore inverso di quello in entrata. Una concatenazione di NOT è semplificabile con un solo NOT in caso di dispari ripetizioni o con nessuno nel caso di pari.

A	NOT A
1	0
0	1

Spesso, al fine di semplificare espressioni complesse, si usano operatori brevi che uniscono l'operazione di NOT ad altre: questi operatori sono NOR (OR + NOT), NAND (AND + NOT), XNOR (XOR + NOT). La negazione, in questi casi, viene applicata dopo il risultato dell'operatore principale (OR, AND, XOR).
Il simbolo di una porta NOT è

OR

L'operazione logica OR restituisce 1 se almeno uno degli elementi è 1, mentre restituisce 0 in tutti gli altri casi. Tale operazione è anche detta somma logica.

A	B	A OR B
0	0	0
0	1	1
1	0	1
1	1	1

Nella teoria degli insiemi corrisponde all'unione.
Il simbolo di una porta OR è:

AND

L'operazione AND dà come valore 1 se tutti gli operandi hanno valore 1, mentre restituisce 0 in tutti gli altri casi. Tale operazione è anche detta prodotto logico.

A	B	A AND B
0	0	0
0	1	0
1	0	0
1	1	1

È possibile realizzare un'operazione logica AND con un numero di proposizioni arbitrarie concatenando varie AND a due ingressi, per esempio:
p1 AND (p2 AND (p3 AND p4))
Nei circuiti digitali, la porta logica AND è un meccanismo comune per avere un segnale di vero se un certo numero di altri segnali sono tutti veri.
Nella teoria degli insiemi corrisponde all'intersezione.
Il simbolo di una porta AND è:

XOR

L'operatore XOR, detto anche EX-OR, OR esclusivo o somma modulo 2, restituisce 1 se e solo se uno solo dei due operandi è 1, mentre restituisce 0 in tutti gli altri casi.

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

Nella teoria degli insiemi corrisponde alla differenza simmetrica. Per passare nella forma canonica SP (somma di prodotti) basta applicare la regola:
A⊕B = A * B' + A' * B
dove ⊕ è il simbolo di XOR.
Il simbolo di una porta XOR è:

NOR

L'operatore NOR, la negazione del risultato dell'operazione OR, restituisce 1 se e solo se tutti gli elementi sono 0, mentre restituisce 0 in tutti gli altri casi.

A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

Il simbolo di una porta NOR è:

composta da un NOT in serie ad un OR.

NAND

L'operatore NAND, la negazione del risultato dell'operazione AND, restituisce 0 se e solo se tutti gli elementi sono 1, mentre restituisce 1 in tutti gli altri casi.

A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

Il simbolo di una porta NAND è:

composta da un NOT in serie ad un AND.

XNOR

L'operatore XNOR, detto anche EX-NOR, è la negazione del risultato dell'operazione XOR; nella sua versione a due elementi restituisce 1 se tutti gli elementi sono uguali a 1 oppure se tutti gli elementi sono uguali a 0.

A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

Il simbolo di una porta XNOR è:

composta da un NOT in serie ad un XOR.

Esempi

Questa algebra ha applicazioni nella logica, dove 0 è interpretato come "falso", 1 come vero, è OR, è AND e è "NOT". Le espressioni che coinvolgono le variabili e le operazioni booleane rappresentano forme dichiarative; due espressioni possono essere equivalenti utilizzando i suddetti assiomi se e soltanto se le forme dichiarative corrispondenti sono logicamente equivalenti. L'algebra booleana binaria, inoltre, è usata per il disegno di circuiti nell'ingegneria elettronica; qui 0 e 1 rappresentano le due condizioni differenti di un bit in un circuito digitale, in genere bassa e alta tensione . I circuiti sono descritti da espressioni che contengono delle variabili e due espressioni sono uguali per tutti i valori delle variabili se e soltanto se i circuiti corrispondenti hanno la stessa funzione di trasferimento. Ogni combinazione dei segnali in ingresso in uscita dal componente può essere rappresentata da un'adeguata espressione booleana
L'algebra booleana a due stati è inoltre importante nella teoria generale delle algebre booleane, perché un'equazione che coinvolge parecchie variabili è generalmente vera in ogni algebra booleana se e soltanto se è vera nell'algebra booleana a due stati. Ciò può, per esempio, essere usato per indicare che le seguenti leggi ( teoremi di consenso ) sono generalmente valide in ogni algebra booleana:

• Il raggruppamento di un generico insieme S, forma un'algebra booleana con le due operazioni = unione e = intersezione. Il più piccolo elemento 0 è l' insieme vuoto ed il più grande elemento 1 è l' insieme S stesso.

• L'insieme di tutti i sottoinsiemi di un insieme S che sono limitati è un'algebra booleana.

• Per ogni numero naturale n, l'insieme di tutti i divisori positivi di n forma un reticolo distributivo se scriviamo per a divide b. Questo reticolo è un'algebra booleana se e soltanto se per ogni n non vi sono divisori quadrati. Il più piccolo elemento,che in generale indichiamo con lo 0, in questa algebra booleana è il numero naturale 1; mentre l'elemento che usualmente indichiamo con l'1 in questi insiemi è l'elemento "n".

• Altri esempi di algebre booleane sono dati dagli spazi topologici: se X è uno spazio topologico, allora l'insieme di tutti i sottoinsiemi di X che siano aperti o chiusi formano un'algebra booleana con le operazioni = unione e = intersezione.

• Se R è un anello arbitrario dove è definito un insieme idempotente tipo:

A = { a in R : a² = a e ax = xa per ogni x in R }
L'insieme A diventa un'algebra booleana con le operazioni ab = a + b − ab ed ab = ab.

Omomorfismi ed isomorfismi

Un omomorfismo tra due algebre booleane A e B è una funzione f: AB tale che per ogni a, b in A:

1. f( a b ) = f( a ) f( b )
2. f( a b ) = f( a ) f( b )
3. f(0) = 0
4. f(1) = 1

Da queste proprietà segue anche f(a) = f(a) per ogni a in A . Ogni algebra booleana, con la definizione di omomorfismo, forma una categoria. Un isomorfismo da A su B è un omomorfismo da A su B che è biiettivo. L'inverso di un isomorfismo è ancora un isomorfismo, e le due algebre booleane A e B si dicono isomorfe. Dal punto di vista della teoria dell'algebra booleana , due algebre booleane isomorfe non sono distinguibili, ma differiscono soltanto nella notazione dei loro elementi.

Espressioni booleane

All'interno di ciascuna algebra di Boole, dato un insieme di variabili e le operazioni correlate, è possibile definire delle espressioni che vengono ad assumere un determinato valore ottenibile anche sotto forme diverse. Possono esistere cioè delle espressioni che, pur essendo differenti, si rivelino equivalenti. Oltre al fatto che le espressioni booleane assumono una particolare importanza per quanto riguarda il calcolo proposizionale, in cui le variabili sono proposizioni legate tramite congiunzioni, disgiunzioni, negazioni ed altre operazioni più complesse, possono esistere moltissime altre espressioni, accomunate sempre dalle proprietà e deagli assiomi booleani, nelle quali si sostituisce spesso l'operazione + (comunemente detta somma) con ∨ e * (comunemente detta prodotto) con ∧ e in cui la complementazione è indicata col simbolo ' .
Per poter presentare nel modo più efficiente una espressione booleana, la si riduce in somma di prodotti fondamentali o forma normale disgiuntiva. Un prodotto fondamentale è un prodotto in cui ciascuna variabile, o il suo complemento, appaia una sola volta e rigorosamente fuori da parentesi o complementazioni complesse.
Ad esempio, date le variabili x, y, z all'interno di un'algebra di Boole, sono prodotti fondamentali

• P(x,y,z) = xy
• P(x,y,z) = x'yz'

Mentre non sono prodotti fondamentali

• yyz
• yy'z
• (xy)'

È così possibile avere una somma di prodotti fondamentali, forma in cui ogni espressione può essere ridotta, ma che non è unica. Un esempio è: xy + xz + z'. Nel momento in cui ogni singola variabile, o il suo complemento, siano contenuti in tutti i prodotti fondamentali della forma normale disgiuntiva, si ha allora una somma di prodotti fondamentali completa o forma normale disgiuntiva completa. Tale scrittura è unica, pertanto se due espressioni sono equivalenti avranno la stessa forma normale disgiuntiva completa.
Se si desidera invece che un'espressione sia scritta nel modo più corto possibile, allora la si esprime in somma di implicanti prime o minimali (Minimizzazione di Quine-McQluskey). Un'implicante prima (o minimale) rispetto a un'espressione è un prodotto fondamentale che non altera l'espressione se sommato per intero ad essa, cioè restituisce un risultato equivalente a quella iniziale; sommando un prodotto strettamente contenuto nell'implicante, tuttavia, non si ottiene un'equivalenza.
Per individuare tutte le implicanti prime, esistono varie tecniche, tra cui il metodo del consenso, che si basa sull'applicazione ciclica delle proprietà di assorbimento, idempotenza, involuttività e di De Morgan accompagnate ad ogni passo dall'opportuna addizione di un consenso. Dati due prodotti fondamentali, se solo e solo se una variabile appare in uno di essi non negata e nell'altro negata chiamiamo consenso il risultato della moltiplicazione delle restanti variabili. Ad esempio:

• dati P = xyz , Q = x'z il consenso sarà C = yzz = yz
• dati P = xy' Q= xy il consenso sarà C = xx = x
• dati P = xyz e Q = x'yz' non esiste consenso, in quanto due diverse variabili appaiono una volta negate e una volta no.

La somma di implicanti prime è unica, pertanto due espressioni equivalenti avranno la stessa. Nel momento in cui, completando ogni singola implicante prima, l'apporto all'espressione di una o più di esse è inutile in quanto contenuta nelle altre, la si può eliminare ottenendo la più essenziale delle scritture, la forma minimale. Essa, pur essendo comoda, ha l'inconveniente di non essere unica, e dunque di non consentire l'individuazione di equivalenze tra più espressioni.

Rappresentazione delle algebre booleane

Si può dimostrare che ogni reticolo booleano finito è isomorfo al reticolo booleano di tutti i sottoinsiemi di un insieme finito. Di conseguenza, il numero di elementi di ogni reticolo booleano finito ha un sostegno che contiene un numero di elementi uguale ad una potenza di 2.
Marshall Stone ha enunciato il celebre teorema di rappresentazione per le algebre booleane dimostrando che ogni algebra booleana "A" è isomorfa a tutte le algebre booleane aperte-chiuse in un certo spazio topologico, detto compatto non connesso di Hausdorff

Voci correlate

• 06-XX, sezione primaria dello schema di classificazione MSC 2000
• Algebra di insiemi
• Diagramma di Venn
• Forma canonica
• Funzione booleana
• Mappa di Karnaugh
• Porta logica
• Sistema formale
• Sistema numerico binario
• Tabella della verità
• Teorema dell'assorbimento
• Teorema di Shannon (elettronica)
• Teoremi di De Morgan
• Progetto:Matematica/Elenco di voci sull'algebra booleana

Collegamenti esterni

• (IT) Panoramica ed esempi sulle Operazioni Booleane

• Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica

Estratto da "http://it.wikipedia.org/wiki/Algebra_di_Boole"

Categorie: Algebra di Boole | Elettronica digitale

Visite

• Voce
• Discussione
• Modifica
• Cronologia

Strumenti personali

• Prova Beta
• Entra / Registrati

Ricerca

 

Navigazione

• Pagina principale
• Ultime modifiche
• Una voce a caso
• Vetrina
• Aiuto

Comunità

• Portale Comunità
• Bar
• Il Wikipediano
• Fai una donazione
• Contatti

Stampa/esporta

• Crea un libro
• Scarica come PDF

Strumenti

• Puntano qui
• Modifiche correlate
• Pagine speciali
• Link permanente
• Cita questa voce

Altre lingue

• Asturianu
• Български
• বাংলা
• Bosanski
• Català
• Česky
• Deutsch
• English
• Esperanto
• Español
• فارسی
• Suomi
• Français
• Galego
• עברית
• Hrvatski
• Magyar
• Bahasa Indonesia
• Ido
• 日 本語
• 한국어
• Lietuvių
• Nederlands
• ‪Norsk (bokmål)‬
• Polski
• Português
• Русский
• Simple English
• Slovenčina
• Slovenščina
• Српски / Srpski
• Svenska
• ไทย
• Tagalog
• Türkçe
• Українська
• 中 文

• Ultima modifica per la pagina: 00:05, 20 mag 2010.
• Il testo è disponibile secondo la licenza Creative Commons Attribuzione-Condividi allo stesso modo; possono applicarsi condizioni ulteriori. Vedi le condizioni d'uso per i dettagli. Wikipedia® è un marchio registrato della Wikimedia Foundation, Inc.
• Politica sulla privacy
• Informazioni su Wikipedia
• Avvertenze